Newton: geringere Masse = größerer Fahrspaß
Große Massen benötigen große Krafteinwirkung, um ihre Richtung oder Geschwindigkeit zu ändern. Grund genug für eine Diät.
Wie definiert sich Fahrspaß? Woher kommt das Gefühl, die Beschleunigung wäre ihr bester Freund? Von wegen Gefühle lassen sich nicht wissenschaftlich ergründen! Mit ein wenig Physik nähern wir uns der Rolle des Gewichts für die Fahrdynamik.
Geradlinige Bewegung
Wie Sie sicherlich noch wissen besitzt eine größere Masse eine größere Trägheit. Das heißt: Um ihre Geschwindigkeit oder Bewegungsrichtung zu ändern, ist eine größere Kraft erforderlich, als bei einer geringeren Masse. Für geradlinige Bewegungen hat Isaac Newton diese Erkenntnis in der Formel
F = m ⋅ a
festgehalten, wobei F die erforderliche Kraft, m die Masse und a die Beschleunigung des Körpers sind. Im Alltag macht sich dieser Zusammenhang bei gefüllten Kofferräumen durch geringere Beschleunigung und Geschwindigkeiten bemerkbar. Natürlich lässt sich auch eine negative Beschleunigung in die Formel einsetzen. Denn nicht nur das Beschleunigen größerer Massen wird schwerer, sondern auch das Abbremsen. Je leichter ein Fahrzeug ist, desto weniger Kraft muss aufgebracht werden, um es zum Stillstand zu bringen.
Drehbewegungen
Dieser Zusammenhang gilt auch für sogenannte Schwungräder (im Fahrzeugbau z.B. Antriebswellen, Achsen, Räder, etc.). Hier gibt das Trägheitsmoment an, wieviel Kraft aufgewendet werden muss, um die Rotationsbewegung zu ändern. Ein höheres Trägheitsmoment bedeutet in der Praxis: Sie müssen länger Gas geben, um eine bestimmte Drehzahl zu erreichen.
Abgesehen von der Größe der Masse eines Schwungrades spielt bei Drehbewegungen allerdings auch die Verteilung dieser Masse eine Rolle. Ein Schwungrad dessen Masse sich möglichst weit weg von der Drehachse auf dem Außenkreis konzentriert, verfügt über ein hohes Trägheitsmoment. Es muss viel Kraft aufgewendet werden, um die Rotationsbewegung des Rades zu ändern. Verlegen wir die gleiche Masse nur näher zur Drehachse hin, nimmt das Trägheitsmoment des Rades ab und es wird einfacher, seine Rotationsbewegung zu ändern.
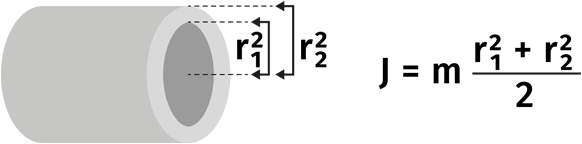
Je weiter ein Massenelement von der Drehachse entfernt ist, desto mehr trägt es zum Trägheitsmoment bei. Der Abstand geht quadratisch in die Gleichung ein.
Es entscheidet also nicht nur das Gesamtgewicht des Fahrzeuges über die umgesetzte Leistung, sondern auch die Verteilung der Massen auf den Schwungrädern.
Größere Räder sehen gut aus, wer es aber übertreibt, verliert an Leistung. Gleiches gilt für die Reifenbreite. Breitere Reifen sorgen für mehr Haftung, erhöhen aber auch die Masse am äußeren Rand des Rades. Wenn Sie genau nachrechnen wollen, empfehlen wir Ihnen diesen Link:
http://www.hpwizard.com/rotational-inertia.html
Die Seite ist zwar in Englisch, führt aber nach Eingabe der benötigten Daten alle Berechnungen zum Thema Trägheitsmoment und Beschleunigung von Automobilen durch.










